常見統計方法：Model selection 模型選擇

 作者：許承越

     photo credit to Unsplash, Scott Graham

醫學與公共衛生的統計部分，通常可以簡化成一個簡單的公式：

Y = A*X1 + B*X2 + C*X3 + D*X4… + ε (常數)

那麼我們在研究資料時，蒐集這麼多資料，我們選定一個我們有興趣的 outcome Y 之後，要如何選擇要把哪些變數當 X 呢？

或者有這麼多變數，到底要選哪些進入我們的 regression model 呢？

這邊列出幾種常見的方式：

• 臨床上有顯著意義的變數（抽煙喝酒之於口腔癌、血中HDL與LDL等膽固醇之於冠狀動脈疾病等）

• 之前研究上有出現過有關聯的變數

• 在自己研究的一系列統計中，有關連的或統計上有顯著意義的變數。例如前面的 tables and figures 中有意義的部分放進來。

• 統計方式：有不同的統計方式可以幫助我們決定要使用哪些變數 / 因子放進統計模型中。

在此簡單列出可以協助我們決定 model selection 的常見統計方法：

• Froward selection: 給定方程式，從 p-value 最小的開始選進 model，直到你給定的 p-value 為止。

• Backward selection: 類似 forward selection，但是是從 p-value 最大的開始從 model 剔除，直到你給定的 p-value 為止

• Akaike Information Criterion (AIC goodness of fit)：推導過程跳過，總之可以協助我們挑選要將哪些X變數放進我們的方程式裡。統計軟體都可以一次建立很多不同模型，然後再去做 AIC 比較。AIC 會在模型複雜度與預估結果的準確度中取得一個平衡；但通常會比較偏向選出較為簡潔的模型，因為研究的目的就是要去看哪些最重要的因子會與我們的結果有相關。可以一次比較多個使用不同變數組合的 regression model，通常會選擇 AIC 值最低的 regression model。請注意，AIC 只能用來比較不同的 models，並不能拿來作為驗證假說使用。

• Likelihood ratio test：看統計模型是否支持某個複雜之regression model（變數較多）優於簡單的regression model（變數較少）

• Residual checking：看是 linear regression model 與 X 們的誤差的多寡

• Leverage checking ：看是否有極端值對於 Y 造成過大的比重與影響

• Variance inflation (VIF) Test：看是否有多個 X 彼此之間的關聯性太大，造成對於 Y 結果的誤差。

不過無論是何種統計方式，都必須考量到現實上的使用。若一個 model 很複雜，需要用到很多不同的因子才能預測 outcome，那麼就算他很精準，因為使用上不方便，我們可能也不會用。

Model selection 應該要在精準度與使用方便度上取得平衡，才能協助我們有效率地進行統計分析以及公共衛生或臨床上的應用。

常見統計方法：選擇變數與基礎統計方式

作者：許承越

     photo credit to Unsplash, Scott Graham

開始進行研究時，可以開始研究數據的分布狀態、以及適合使用的統計方式。以下只會簡單列出簡單的前提與適合使用方法，不會有公式的推導過程，因為只是希望可以分享讓大家可以參考適合使用什麼方式。

我習慣使用的統計軟體是 STATA，但每個人喜歡或習慣使用的軟體不同，我也沒有精通不同統計軟體，所以就沒有在這裡放上要怎麼輸入語法或指令的教學了。幾個常見的統計軟體，在其官方網站或 youtube 上，應該都已經有很多比我更專業的教學可以參考。

醫學與公共衛生的統計部分，通常可以簡化成一個簡單的公式模型（model）：

Y = A*X1 + B*X2 + C*X3 + D*X4… + ε (常數)

Y 是我們想要得知的 outcome，也就是 Response variable。

X (X1, X2, X3, X4…) 則是我們手上可以確定的變數，也就是Explanatory variable。

關於Variables 種類，可以參考我的文章：什麼是 variable。

首先，確認 variables 們是什麼型態（continuous, discrete, dichotomous, ordinal，等等）

先觀察數據分佈狀態（可以使用 Histogram、QQ-plot、Scatter plot 等工具），再來決定要用什麼型態來處理工具。

選擇變數的分析方式

理論上只要樣本數夠大，continuous variables 基本上大概都會呈現常態分佈。有些統計方式也要求前提是sample的母群體需要符合常態分佈。

若要決定樣本分佈是否屬於常態分佈，可以使用 Kolmogorov-Smirnov Test （樣本數 > 50時使用）以及 Shapiro-Wilk Test （樣本數 >= 50 時使用）。

若不符合常態分佈，可以探討原因（是否有特殊原因或自然限制使得 variable 不為常態分佈）。為了統計方便，也可以自己設定有意義的切點、或是臨床上常見有統計意義的切點，將 continuous variable 變成 dichotomous or ordinal variable，以方便統計。

例如我想研究baseline腎絲球過濾率 eGFR 對於肺炎患者住院天數的影響，則 Y = 住院天數， X = eGFR。但是 X 可以以 continuous variable (eGFR)、以 dichotomous variable （抓CKD = eGFR < 60的切點，變成有 CKD versus 沒有 CKD）、以 ordinal variable （CKD stage I到 stage V，通常都會選擇最高或最低的X來做reference比較）來做分析。

只是要記得，如果使用 ordinal variable 來處理的話，X值 多加 1 ，實際上對 Y 的影響不一定等於1。例如 CKD stage I 到 stage V，每多一個 stage，肺炎患者的住院天數不一定會呈現等差或等比增加。這就要看臨床狀況再去做調整了。

基礎統計方式的選擇

在這裡簡單列出一些常用的統計：

資料屬性	兩群 獨立樣本	三群 以上獨立樣本	相關	前後測比較
Continuous、或是有母數、符合特定分佈	Independent t-test (兩組獨立樣本)	ANOVA	Pearson Correlation	Paired t-test (兩組樣本非獨立)
Ordinal、或是無母數、無符合特定分佈	Wilcoxon Rank Sum Test (Mann-Whitney Test)	Kruskal-Wallis Test	Spearsman's Correlation	Wilcoxon signed-rank test
categorical	Chi-Squared Test (X²) Fisher's exact（小樣本時使用）	Chi-Squared Test (X²)	Chi-Sqaured Contingency Coefficient	McNemar 's Test

這邊簡單整理了一下各種常見的統計方式比較。有些統計方式不常用到，但大家可以比較簡略地記，樣本數夠大，可以假設是常態分佈。

如果要比較的話，continuous variables 就用 t-test （2組比較）或 ANOVA 比較（3組或以上比較）。Categorical variable (包含Dichotomous variable）就用Chi-squared test。

Null hypothesis, p-value, type 1 & type 2 error.

 作者：許承越

     photo credit to: unsplash, Antoine Dautry

現代科學的進行過程，可以簡單分成：發現或觀察到問題→提出假說→以各種實驗方式驗證假說→分析與解釋結果→假說成立或假說不成立→得出結論。

提出假說的過程，有個很重要的概念：虛無假說（Null hypothesis）。這邊要簡單介紹什麼是虛無假說 (Null hypothesis)。

Null Hypothesis

通常單一論文一次就探討一個問題，而每個問題，通常都會有相對應的假說。在分析問題時，我們通常會以這個假設的「反面」或「否定」來做假設。顧名思義，稱為虛無假說。

例如我們假設，「喝咖啡會增加得到乳癌的機率」，則虛無假說應該是：「喝咖啡不會增加乳癌的機率」。在這個虛無假說的前提之下，我們再利用實驗結果與統計分析去驗證這個假說。

如果虛無假設成立，則我們可以說，「虛無假說無法被推翻」，進而得出結論是「喝咖啡不會增加得到乳癌的機率」。

反之若虛無假設不成立，「虛無假說被拒絕」，則或許我們可以推論「喝咖啡可能會增加得到乳癌的機率」。

同理，如果我們假設，「每天都喝一杯柳橙汁會降低心肌梗塞的機率」，那麼虛無假說應該是「每天都喝一杯柳橙汁不會降低心肌梗塞的機率」，再利用實驗去推論。

或者我們如果假設，「城市空氣污染指數超標與居民高血壓的比例有關係」，則我們的虛無假說就會是「城市空氣污染指數超標與居民高血壓的比例沒有關係」。

不過對於科學中尚未瞭解的領域，單一實驗的結果很難讓人直接定論因果關係，所以仍然需要進行各種不同的研究與統計，才能得出比較有說服力的結果。

P-Value

至於在統計上，最常見認定統計是否可信（也就是常看到的統計上顯著意義）的方式，就要用到大家耳熟能詳的 p-value 了。

大家可以把 p-value 理解成：虛無假說為真時，與研究使用的實際樣本出現相同極端值的機率。P-value 越小，在虛無假說下觀察到極端結果機率很小。一般有意義的切點，統計學上會抓 p-value = 0.05。

還是有點繞口？也可以用維基百科的定義去說明：「p-value 是原假設為真的時候，所得到的樣本觀察結果或更極端的結果出現的機率」。

「p值是基於數據的檢定統計量算出來的機率值。如果p值是5%，也就是說，如果以此為界拒絕原假設的話，那麼只有5%的可能性犯錯。原假設是對的，但卻拒絕了，這是錯誤的。所以說p值越大，拒絕原假設的理由越不充分。如果p值接近於0，拒絕原假設，那麼幾乎不可能犯錯，於是說明數據是極其不符合原假設。換言之，是假說檢定中虛無假說成立或表現更嚴重的可能性。p值若與選定顯著水準（0.05或0.01）相比更小，則虛無假說會被否定而不可接受。」（擷取自維基百科，連結在此。）

當然，並不一定是只要 p-value 就絕對正確不可質疑。在許多自然界中觀察到的結果呈現連續常態分佈時，95%的數值會涵蓋在平均數+/-1.96個標準差（通常是大概取2個標準差）的範圍內。
所以我們習慣會說 95% 信賴區間（95% Confidence interval），也就是這個範圍有95%的機率會包含到實際正確的值。

請注意，95%信賴區間的意思並不是實際正確的值有95%的機率會落在這個範圍內；因為用這種描述方式會讓人誤以為實際正確的值是一個跳動的、變動的值。正確說法應該是這個範圍有95%的機率會包含到實際正確的值。

當然也有5%的機率，數值會落在平均數+/-1.96個標準差之外。在統計上，也有可能是樣本數不夠小，導致 p > 0.05、甚至是統計的方法不適合時，也會跑出各種與現實悖離的狀況。

但在現行的統計上，在大部分情況中大家還是可以簡單把 p-value < 0.05 視為統計上有顯著意義。現行的論文與科學研究結構基本上也以此為依據，短期之內或許很難馬上改變。

因此，邏輯可以簡單想成：

有問題→提出假說→建立相對應的虛無假說→ p-value < 0.05，則虛無假說不成立，因此我原本的假說可能是成立的。

或是

有問題→提出假說→建立相對應的虛無假說→ p-value > 0.05，則虛無假無法被推翻，因此我原本的假說可能沒辦法成立。

Type 1 Error and Type 2 Error

但萬一虛無假說為真的狀況下，得出的結論卻是虛無假說不成立、或者虛無假說不成立時，我們的結論卻是虛無假說成立的話呢？以下表格解釋了幾種可能發生的狀況：

有點複雜，但大家可以速速理解成：

Type 1 Error: 我（或任何其他生理男性），去驗孕，結果被驗出懷孕的機率：偽陽性。

Type 2 Error: 懷孕婦女去驗孕，結果被驗出沒有懷孕的機率：偽陰性。

Type 1 Error 以及 Type 2 Error都是研究中應該避免的部分，而使用有效的統計工具或實驗技術，就可以大大降低這兩者發生的機率。

而關於檢驗工具的陽性與陰性，可以參考我之前寫的文章：試驗的陽性與陰性。

常見統計方法：Regression model 迴歸模型

 作者：許承越

     photo credit to Unsplash, Scott Graham

醫學與公共衛生的統計部分，通常可以簡化成一個簡單的公式模型（model）：

Y = A*X1 + B*X2 + C*X3 + D*X4… + ε (常數)

生物統計學藉由不同的變數 / 因子 X ，來預測結果 Y。對於很多不同疾病的已知危險因子，大致上都是使用不同類似這樣的統計分析 ，反覆驗證出來的結果。

而常用的統計方式，有兩種，一種是 regression models，一種是 time-to-event analysis。這篇文章介紹 regression model。

Linear regression

Y 是一個 continuous variable。可以是身高、體重、血壓值、血糖值、或其他任何以連續狀態呈現出的數值。

跑完統計的結果，X的係數（A, B, C, D…）是 Risk difference，也就是Ｘ每多 1，Y的結果會相差多少。

在要使用 Linear regression 前，有一些前提與假設必須被滿足：1. 變數之間是獨立的、2. 變數符合特定的分佈狀況、3. Y 的結果會由不同的變數 X 組成的一個函式變化受影響、4. Y 的結果會受 X 的影響。

在進行 linear regression 前，我們可以使用 Correlation 來看 X 與 Y 之間的關聯性。Correlation 的意義是，兩個不同變數之間呈現 linear relationship 的程度。

跑完統計以後會有個 Correlation coefficient r，也會有個 p-value （一樣 p < 0.05 通常就會代表有統計上顯著意義）。 r 的值會落在 1 到 -1 之間的區間：-1 < r < 1。

1 是 100% 完全正相關，-1 是 100% 完全負相關。r 值大小的有效程度，通常會認為 r < 0.2 沒有太大意義，0.2 < r < 0.4 有弱相關，0.4 < r < 0.6 有中度程度的相關，0.6 < r 就算有一定程度的相關，不過還是要看實際使用情況跟探討內容而定。

常見的有兩種，Pearson’s correlation，以及 Spearman’s correlation。

Pearson’s correlation 評估兩者之間呈現 linear relationship的關係，也就是兩者之間的散佈圖上，有哪條直線最能代表兩者之間的關係。

Spearman’s correlation  評估兩者之間的關係，不一定要是線性的，可以是彎彎曲曲的（Monotonic relationship）

這個網站的作者有對於兩者之間圖片的比較，大家可以參考看看。

Logistic regression

Y 是一個 dichotomous variable。可以是有癌症/沒癌症、有懷孕/沒懷孕、死亡/存活、有發現/沒發現，等等。跑完統計的結果，X的係數（A, B, C, D…）是 Odds ratio（因為公式限制的關係，通常要用log以後才是 Odds ratio，不過大部分統計軟體有自動轉換的功能，所以可以記跑完的結果是 Odds ratio。）

又因為 logistic regression 實在太好用也太常見，所以後來統計學上又發展出幾個相關的統計技巧。 Logistic regression model 的 Y 是 0 or 1 的組合（有生病/沒生病、死亡/存活）等，所以如果適合的 logistic regression model 可以用來判斷陽姓與陰性。

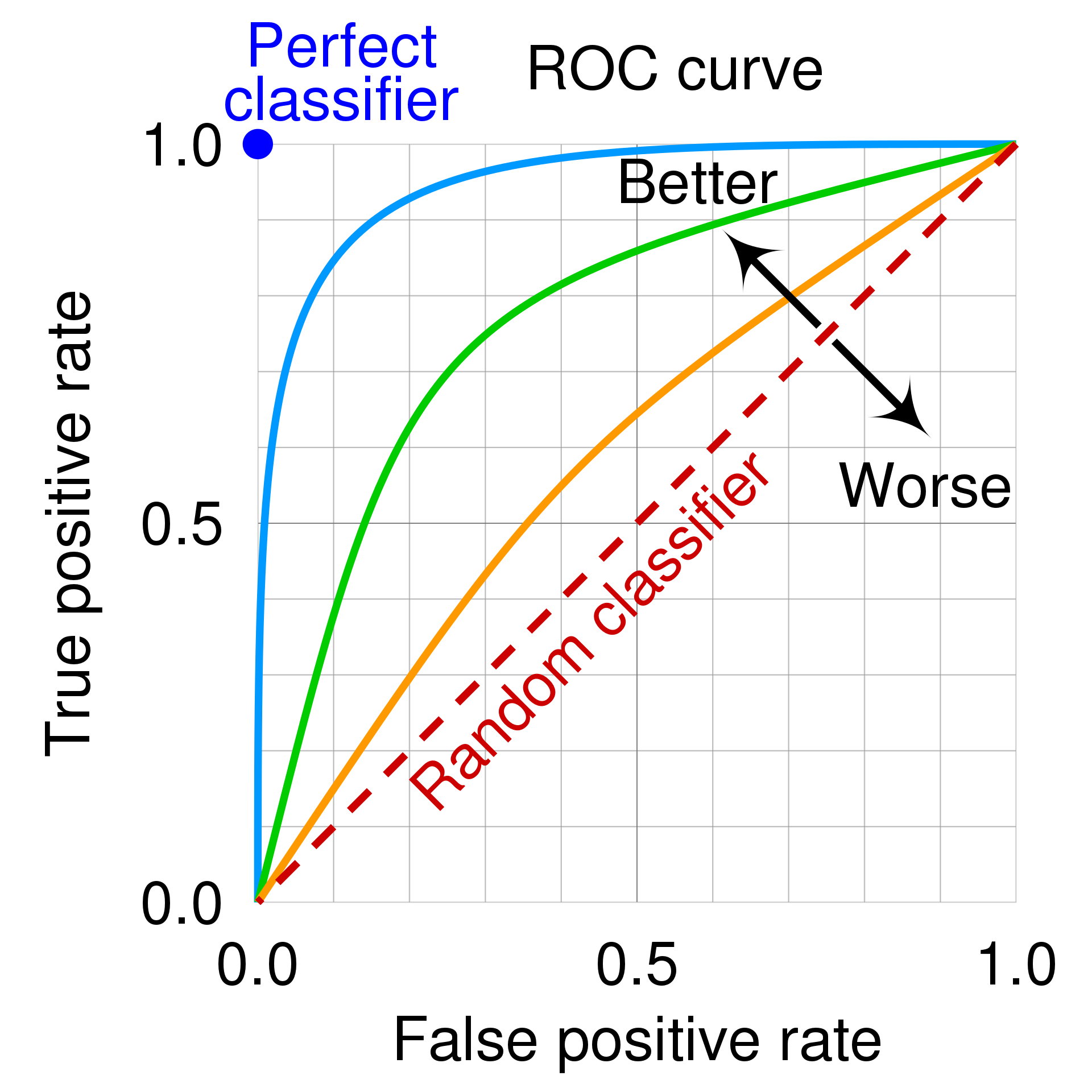
但是會牽涉到判讀工具的 sensitivity （有病的人被正確地診斷為有病的機率）以及 specificity （沒病的人被正確地診斷為沒病的機率），而這邊可以使用的工具就是 ROC 曲線（Receiver Operating Characteristics curve）。

大家可以簡單記得，ROC curve 下面的面積（Area under the curve, AUC），也就是 C-statistic，的意義是，從樣本裡面隨機抽取一個確診的人以及一個沒有確診的人，使用這個工具來正確診斷確診者的數值高於沒有確診者的人之機率。所以如果 ROC 曲線面積越大，代表效果最好。

photo by Wikipedia, cmglee, MartinThoma - Roc-draft-xkcd-style.svg, CC BY-SA 4.0, (https://commons.wikimedia.org/w/index.php?curid=109730045)

ROC曲線 Y 軸是 sensitivity，也就是將有病者正確診斷出有病的機率。X 軸是 1-specificity ，也就是將沒病者診斷為有病的機率，也就是偽裝陽性。我們希望 sensitivity 越高，而 1-specificity 越低，因此 ROC 曲線若越靠近圖片的左上角，則越有說服力。

此外，使用 logistic regression 也可以計算出，將X1, X2, X3,... 到 Xn 帶入 logistic regression model的公式時， Y = 1 （也就是得到我們想要的結果時）的機率。計算方式的推導有點麻煩，有興趣的話可以再上網找找看。總之可以先記 probability = e^(regression model)/(1+e^(regression model) ) 就好。

Log-binomial regression

Y 是測 Risk 或 Prevalence。也就是測一個群體中的疾病發生率或盛行率。跑完統計的結果，X的係數（A, B, C, D…）是 Risk ratio 或是 Prevalence ratio。

Poisson regression

Y 是 Incidence rate，有把時間的概念涵蓋進去。跑完統計的結果，X的係數（A, B, C, D…），是 incidence rate ratio。

Ordinal and Multinomial regression model

Y 是 ordinal variable（順序變數，例如滿意度從 1, 2, 3, 4, 5）或是 multinomial variable（例如紅色、藍色、黃色，或者是居住地為台北市、台中市、台南市、高雄市等等，沒有順序大小上差別的 variable）。X的係數（A, B, C, D…）是 Odds ratio，但因為 Y 性質的關係，在解讀時要小心，因為通常是把 Y 中選擇最小或是最大的值當作 reference 來比較，一般而言在流行病學的研究中不是那麼常見。

Regression model 的使用

依據 outcome Y 的不同，每個 X 前面的係數，則在不同的 regression model 中代表著不同的意思；統計軟體通常會給一個係數的 95% 信賴區間 (Confidence Interval, CI）以及 p-value。這邊也可以簡單記 p-value 若 < 0.05 就是統計上這個係數有顯著意義；而如果統計上有顯著意義的話，95% CI 則不會涵蓋到 1 的數值（odds ratio, incidence ratio 等不等於 1 才代表有差別）。

如果是正向影響（positive effect），則係數會大於 1，但如果是負向影響（negative effect），則係數會小於 1 。唯一例外是 Linear regression 有統計上顯著意義的話代表 95% CI 不會涵蓋到 0 的數值（因為 linear regression 中 係數是代表 rick difference，若相減不為 0 才代表有意義）。

對於只需要統計簡單應用的基礎使用者，只要記得不同 regression model 中的係數代表什麼意思，以及 logistic, log-binomial, poisson 等三個 regression model 的係數都是 log 化，但統計軟體可以幫我們將之指數化成我們要的結果。

此外，如果想要研究 variable Xs 之間的交互作用，也可以納入 interactive terms，例如：

Y = A*X1 + B*X2 + C*X3 + D*X1*X2

則 D 的意義就是當 X1 和 X2 同時存在時對於Y的影響，比 X1 或 X2 單獨存在時對 Y 的影響還要多多少。

又或者有時候想要知道某個變數經過特定的譽職後或有不同的影響，例如兒童的身高生長速率進入青春期以後會迅速增加，則可以改成：

Y = A*X + B*(X-12)

但在這邊通常會定義 

If X1 > 12, 則用 X1-12帶入

If X1 <= 12, 則 X1-12 = 0

則 B 的意義就是 X 在 12 之後對 Y 的影響，比 X 在 12 之前多多少。也可以理解成當 X < 12 時，每新增 1 單位的 X，Y 受影響的幅度是 A，但是當 X > 12時，每新增 1 單位的 X，Y 受影響的幅度就是 A+B。這常見在有曲折的分佈上，或是在臨床上經過某個特別有意義的切點後，會有不同影響的變數。

常見統計方法：Survival analysis 生存分析

 作者：許承越

     photo credit to Unsplash, Scott Graham

流行病學中另外一個重要的研究方式，是Survival analysis。

顧名思義，就是研究受試者從特定/研究觀察時間開始，到 outcome 發生為止（通常是發病時間）的「存活」狀況，以及哪些因子會影響這些存活狀況與發病時間。

也因此，在統計進行時，需要所謂的 time-to-event data，也就是必須要把從特定觀察時間開始到觀察結束或是發病為止，經過了多少時間。

這種方式很常用在 prospective and continuous 的研究中，也就是當研究者招募一群受試者後，測量他們身上的各種變數與因子，或者提供不同程度的介入治療等等，並觀察這些受試者一群時間，最後去研究發病者與未發病者身上的差別。

Y = A*X1 + B*X2 + C*X3 + D*X4… + ε (常數)

只是這邊，Y 就變成了「到達outcome發生為止的時間」，也就是「time-to-event variable」。

Kaplan-Meier survival analysis

由 Kaplan 以及 Meier 兩位統計學者發展出來的方法，目前很常用。可以單看一個族群的存活狀況（也就是到發病為止的時間點），也可以比較不同受試組別間的存活狀況。

Kaplan-Meier 在比較不同組織間的差別可以使用 log-rank test 去比較（一樣如果 log-rank test p-value < 0.05 可以代表統計上有顯著差距）。

但如果要使用 Kaplan-Meier survival analysis，需要有幾個假設：1.  Outcome 發生率，在我們可以觀察到的病人與 lost-of-follow-up 的病人，是相同的（例如，失智症患者用藥對於延緩失智症的幫助，有可能會繼續 follow up 的患者本身失智症的狀況就不是很嚴重才有辦法繼續回診求診，有可能造成誤差，要謹慎處理）、2. 無論在什麼時候被研究者開始觀察的病人，outcome 發生率是相同的（也就是無論什麼時候 outcome 發生率都是相同的）、3. 不同受試者繼續被觀察與研究的機率是相同的（可以想成要是不同受試者 lost-of-follow-up的機率相同）、4. Outcome 發生機率在觀察期中沒有劇烈的變化。

上圖為我自己之前練習做的 Kaplan-meier curve。在每個曲線往下的點，就代表有受試者發生了 outcome。統計軟體通常也可以在下面的空間呈現出在每個往下的點，有多少 outcome 發生，以及剩下多少還在 follow up 的試驗者；不過很多期刊通常為求畫面簡潔，這部分就不會放，以文字敘述即可。

Cox-regression models

主要是去看到特定時間點前，不同變數因子對於受試者在單位時間內發病（也就是抵達 outcome）的機率做比較，可以理解成不同變數與因子對於 incidence 的影響。

跑完統計的結果。

X的係數（A, B, C, D…）的意義是 Hazard ratio（HR），為增加 hazard ，也就是單位時間內 outcome 發生的機率。

可以理解成不同變數與因子對於 incidence 的影響。而 Cox regression model 又被稱為 Cox proportional hazard regression model，就是假定研究的變數與因子（也就是 X 們），對於 time-to-event / incidence rate 的影響，在受試與觀察的過程中，都是成固定比例的。（Hazard function is proportional over the observation time）

Grouped data, life-table analysis, and log-linear Poisson regression

跟 Kalpan-Meier 或是 Cox 最大的不同就是，Life-table analysis 使用的是 grouped data。Grouped data 的意思是說，我們將 time-to-event 切成一段一段的 discrete time interval(or time bin)然後再利用 Life-Table estimates or log-linear Poisson regression 去分析。原始Data 可以是 continuous，但是我們可以把它變成grouped data。

Kaplan-Meier 分析跟統計的是 outcome 發生的確切時間點；相對的，Life-table analysis 分析時並不需要去知道 outcome 發生的確切時間點。只要知道被切成一段一段的不同時間段中， outcome 發生的比例就可以進行統計分析。

Poisson regression 的 Y 會是 incidence rate，所以 X 的係數就代表 incidence rate 的差異，但因為數學公式的關係，在取 log 後就會變成 incidence rate ratio，也就是 X 每增加或減少多少，incidence rate 會有幾倍（或幾分之幾）的影響。

Bias, confounder, and effect modifier

作者：許承越

     photo credit to: unsplash, Ruthson Zimmerman

進行統計分析時常有幾個變數會對統計結果有很大的影響，分別是

• Bias 偏差
• Confounders 干擾因子
• Effect modifiers 效果修飾

Bias 偏差

Bias 最容易理解，可以翻為偏差，又可以簡單分成

• Information bias
• Selective bias
• Recall bias
• Survival bias 

Information bias 是指觀察與收集資料時導致的誤差，造成結果測量時的不可信與缺陷。

Selective bias 是指因為研究者主觀（或不經意的）在收集試驗者的資料時，特別收進特定類型的族群，結果造成統計上的偏差。例如

Recall bias 受試者在進行資料回報與登記時，因為受試者的主觀感受，會容易不自覺地誇大或誤報自己的經歷或感受。例如之前研究流產或畸胎的研究時，有物質成癮的婦女通常會在登記之前資料時回報自己比平常用的藥物/酒精還要多的量給受試者。

Survival bias 想要研究某種疾病，卻發現能篩選到的族群都是健康的族群。例如二戰初期美軍飛機轟炸德國，結果轟炸機隊在面對防空火砲與德軍戰機時損失慘重。專家學者開始研究成功返航的轟炸機，發現轟炸機的機翼跟其他部位相比有最多受攻擊的彈孔殘留，因此決定強化機翼結構與保護，但後來才驚覺到，能成功返航的轟炸機就是因為都只有被打到機翼的部分，因為如果被打到其他部分（引擎、駕駛艙）等等，早就解體或墜機了。

Confounder 干擾因子

Confounder又被翻譯成干擾因子。在做研究時，我們希望研究特定危險因子與我們有興趣的結果之間的關聯。但是若有一些confounder 同時與特定危險因子與我們有興趣的結果之間都有關係的話，很有可能就會影響到統計的結果。

最有名的例子是咖啡跟肺癌。自20世紀中後葉開始，專家學者們開始發現肺癌的發生率與比例開始節節上升，但是還未有個定論，因此大家開始去研究到底哪些東西跟肺癌有關係。

有學者發表論文，說咖啡喝很多的人也有很高的機率會有肺癌！但後來才發現，原來是因為做研究的時空背景下（1960-1970年代的美國）會喝咖啡的人大部分也都會抽煙，所以才造成大家以為統計出來咖啡跟肺癌有關係。

在這個例子中，咖啡就是 confounder。然而在面對未知領域時，confounder到底是哪個東西其實很難馬上判定，所以只能藉由不停用各種測試方法去反覆驗證。

而當我們懷疑某個變數是 confounder 時，就應該要用不同方式去控制他，讓大家的變數都盡量相同，再繼續去做實驗/對照組的比對。

常見有幾個 Controlling for confounders 的方法，簡單介紹如下：

• Restriction：收集 data 以及招募受試者時，全部都只招募具有某項你懷疑是 confounder 的因子的受試者（或是反過來，只招募沒有某項你懷疑是 confounder 的因子的受試者）。
• 優點：相對容易執行。
• 缺點：Sample size 容易因此受限、無法控制其他可能的 confounders。
• Matching：每個實驗組的受試者，都有一個對應的對照組的受試者；這兩者的某項你懷疑是 confounder 的因子都是一樣的（同樣具有、或是同樣沒有這個因子）
• 優點：每問受試者都有相對應的人可以比較。
• 缺點：很難每個實驗組與對照組的受試者都完全可以配對成功。
• Statistical control：用統計學的方式來讓 confounder 的影響降低。常見的有兩種
• Regression model：將某項你懷疑是 confounder 的因子放進 regression model 中，這樣就可以用不同統計技巧來控制這個因子。
• Propensity score：一般的 regression model可以寫成Y = A*X1 + B*X2 + C*X3 + D*X4… + ε (常數)。但假設我們認為 X1 是 major risk factor，而且 X1 是 dichotomous variable的話，那麼我們可以新設立一個 logistic regression model: X1 = B*X2 + C*X3 + D*X4… + ε (常數)，並且利用 logistic regression model 的特性，去計算帶入不同X因子時，X1 的 probability ，最後依照 probability 的高低得出一個「propensity score」。Propensity score 的目的是要在其他 Xs 在被控制的狀況下，去分析 major risk factor X1 與 outcome Y 的關係。
• 優點：方便執行、可以在搜集好資料要開始跑統計時再進行。
• 缺點：只能處理已知的 potential confounders、無法處理未知的 potential confounders。
• Randomization：使用電腦軟體或亂數表，將受試者隨機分配，也就是隨機將受試者分配到實驗組與對照組。讓某項你懷疑是 confounder 的因子對於研究結果的影響降到最低。
• 優點：很有效力、如果有些無法觀察到的 confounder 也可以一併藉由隨機分配的關係將影響降低。
• 缺點：較難執行、經費花費可能較高、必須在開始 data collection 以前就先分組好。

Effect modifiers 效果修飾

某個因子存在時，搭配上別的因子存在時，會有比兩者各自單獨存在時，對於結果有更強的效果。

可以簡單理解成同樣要煮雞湯，加入鹽會讓雞湯更好喝、加入香菇也會讓雞湯更好喝，但是「同時加入鹽及香菇的美味度」，比「只加鹽的美味度」與「只加香菇的美味度」多出很多，可以理解成 Effect Modifiers。

也可以這樣理解：比起不抽煙的人，抽菸的人得到口腔癌的機率多18倍。比起不吃檳榔的人，吃檳榔的人得到口腔癌的機率多28倍。

比起不抽煙不吃檳榔的人，如果抽菸又吃檳榔，得到口腔癌的機率高了89倍（高雄醫學大學葛應欽教授 1995 年發表於「口腔病理學及口腔內科學雜誌」），那麼我們可以考慮說檳榔在抽煙對於口腔癌的效果上，是 effect modifiers；或者兩者具有 synergistic effect 。

兩者有正向加成效果，則稱為 positive synergistic effect。若兩者有負向加成效果，則稱為 negative synergistic effect。

常見的方式是在 regression model 中放入 interactive term。（放入連結）

Bias 以及 confounders 是我們在做研究中不可避免會遇到的問題，但我們仍然要盡量用各種方法去減少 bias 以及 confounders 的影響。Effect modifiers 卻是我們在研究中希望可以發現以及好好深入探索的因子，因為我們可以對我們有興趣的結果的各種作用路徑與發生過程有更多了解。

Population

作者：許承越

     photo credit to Unsplash, Ryoji Iwata

流行病學與生物統計學的研究，在我們觀察與提出問題、建立假設、收集數據以後，就要進行統計的部分。

統計的目的，就是希望可以用我們手上的 sample，觀察到特定的狀況或結果，再進行推論到整個大群體（Target population）。

實際招募受試者的狀況可能是：Target population → Source population → Sample (studied) population。

藉由訂立目標，去招募受試者、取得資料，最後用篩選過的 sample 去做分析。

而我們可以推論的方式是：Sample (studied) population → Source population → Target population。

利用篩選過的 sample 統計與分析後的結果，做合理的推論，並反推到 target population 上。

Sample population 是我們有確切數據可以觀察、介入、與研究的對象。Source population 是我們選擇 Sample population 的來源，也是有合理依據可以推論 Target population的群體。Target population 則是廣義的我們想要研究的對象。

例如我們想知道2010-2020年雙北地區女性居民的子宮頸癌發生率，那麼可以這樣設定 population:

• Target population: 2010-2020年雙北地區的女性居民

• Source population: 2010-2020年雙北地區曾經至各醫療院所接受子宮頸抹片或其他檢查的女性居民

• Sample population: 2010-2020年雙北地區曾經至各醫療院所接受子宮頸抹片或其他檢查的50歲以上女性居民，且願意接受我們研究團隊的進一步病史詢問與抽血檢驗以及參加研究計劃。

Population ，尤其是 sample population，一定要有很清楚的 people, place, time 等三個要素，才比較有科學上的說服力來做比較。

而無論是從 Target 到 source ，或者從 source 到 sample的篩選過程，或許都會影響我們的研究結果，在進行資料搜集時需要小心處理。

決定樣本數量是否足夠，有 test for sample sizes，不同統計軟體都可以，可以善用。

Measurement of association

作者：許承越 

     photo credit to: Unsplash, William Warby

Prevalence 盛行率

某個固定時間點，特定族群中有某疾病的比例。單位是百分比。

Incidence 發生率

在一段時間內的某個族群，新發病的比例。單位通常是 person-time。例如追蹤一百個人總共一年的時間，有一個人發病，那麼 incidence 就會是每年每一百人中會有1人得到，可以寫成 1% per person-year。Incidence 有將時間的概念涵蓋進去。

Odds 勝算

某事情發生的機率 / 某事情不會發生的機率，相除的比值。

在有病的人中，有暴露到特定危險因子 / 沒有暴露到特定危險因子的比例。

或是在有暴露到某個特定危險因子的人中，有病的人 / 沒有病的人的比例。

Odds ratio 勝算比

在有病的人中，有暴露到特定危險因子 / 沒有暴露到特定危險因子的比例，比上在沒有病的人中，有暴露到特定危險因子 / 沒有暴露到特定危險因子的比例。

在有暴露到某個特定因子條件中，有病的人 / 沒病的人的比例，比上在沒有暴露到某個特定因子中，有病的人/沒病的人的機比例。

OR 之所以那麼常用，就是因為他是個偉大的發明。

不管我們想看哪種 OR：

發病中，有暴露到特定因子者 / 沒有暴露到特定因子者的比例，再去除以沒有發病者中，有暴露到特定因子者 / 沒有暴露到特定因子者的比例，的比例。= (A / C) / (B / D) = A * D / B * C

還是

有暴露到特定因子者中，有發病者 / 沒有發病者的比例，再去除此沒有暴露到特定因子中，有發病者 / 沒有發病者的比例，的比例。= (A / B) / (C / D) = A * D / B * C
最後的結果會是一樣的！

而且在機率很低（通常抓 < 10%）的時候，Odds ratio 通常可以直接當成 prevalence ratio 或是 incidence ratio。因為當 A 很小的時候，我們在初階微積分中學過， A / A+B 中，分母中的 A 可以忽略，把他當成 A / B 即可。

Hazard 危險（或翻譯成風險）

每單位時間內，事件發生的機率。常用在 Cox proportional hazard regression model 中。

Hazard ratio 危險比 or 風險比

Cox proportional hazard regression model 中常用，就是假定研究的變數與因子（也就是 X 們），對於 time-to-event / incidence rate 的影響，在受試與觀察的過程中，都是成固定比例的。（Hazard function is proportional over the observation time）

Standardization 標準化

不同的族群可能會受到性別、年齡、種族等等條件的影響，造成某特定疾病 / outcome 的衡量會有族群間的差別。這時候就可以使用 standardization。

又可以分為 direct and indirect。最常見的就是族群間的死亡率會受不同年齡層人口分布的差別。Direct stnadardization 是將標準化族群是將標準化族群（例如教科書範本、政府數據等）的不同年齡層間的死亡率，算到 sample population 中，再去看這樣的死亡率是如何。

Indirect standardization 則是可以在 sample population 的資料未明確或是沒有特定年齡群的資料時，算不同年齡層的死亡人數，並且去與標準化族群的死亡人數做比較。最後會得到 實際上觀察到的死亡人數 / 用標準化族群來看的預期死亡人數，去看是否有異常。

Direct 是算 rate，indirect 是算 number。

常見研究目的簡介

作者：許承越

     photo credit to: unsplash, UX Indonesia 

常見研究目的簡介

流行病學、公共衛生、醫學的研究，可以分成幾種大致上的目的。

在我們發現問題並且要試著去回答問題的過程，有幾個常見的解決方式與思考邏輯。常見的步驟有幾個，分別是 risk factor analysis，causal models，prediction models。

Risk factor analysis

發現一個問題後，去研究哪些危險因子到底與這個問題有關聯性。例如最簡單的方式，就是定義出可能有關聯性的危險因子，並一個一個去分析哪些到底有真正的關聯性與其背後可能原因。

在描述完可能的危險因子後，我們便可以提供後續的研究方向與建立假說。

一來可以增加我們對要放哪些危險因子到我們未來的統計學模型中做論證，二來可以讓我們對於哪些危險因子可以預測特定疾病與問題有更多的把握。

在此類型的 table 1 中，可能會列出有特定疾病 vs 沒有特定疾病的受試者各種 baseline 基本數據與實驗室數據等資料，去看哪些有顯著差距；並進而從這些差距中做後續的推論。

也就是以客觀的方式去「描述」並整理手上的數據；這個過程是產生各種假說與研究想法的重要基礎。

Causal models

進一步建立 regression model 或是 survival analysis；在建立的過程中，應該要移除可能會對於我們有興趣的危險因子與特定疾病 / outcome 間因果關係造成干擾的 confounders 以及 bias。

在 Causal models 中，會特別去注意是否有 effect modifiers 以及 interaction 的存在。

（關於 bias, confounder, and effect modifier 可以參考我之前的文章。）

建立過越來越多的 causal models，我們才會比較有把握知道 A 與 B 間的關係到底為何，以及是否會受到其他因子的干擾與影響；與 risk factor analysis 相似但可以更進一步的協助我們建立假說。當我們掌握的程度越高，也才可以協助建立後續的 prediction model，來進行公共衛生與臨床治療上的評估與治療。

（至於 cause 到底要怎麼定義，也可以參考我之前的文章：）

Prediction models

預測模型，也就是利用手上可以獲得的有限資料（患者基本資訊、病史、抽血數據等），去判斷特定疾病 / outcome 的發生機率或是預後。

判斷發生機率，使用 diagnostic models。

判斷疾病的預後，使用 prognostic models。

無論是 diagnostic models 還是 prognostic models，目的都在於協助公共衛生工作者或是臨床醫護人員做出判斷。

建立完 prediction models 以後，也可以用不同的方式去驗證 model 的效力，例如 internal validation （用同一組 sample 或同個 cohort 中其他受試者亂數分配等方式，來驗證 model 的效力）或是 external validation（直接用真實世界中或其他研究的 sample or cohort 的受試者資料來做驗證）。

例如，根據這個患者的性別、年齡、身高體重、慢性病史、家族病史、抽血報告等等，我要怎麼知道他 10 年內得到心肌梗塞的機率？多少機率以上算高？

根據機率的高低，我們會使用不同種類的治療方式，也就是所謂的 intervention，來避免患者的狀況惡化或是復發。

或者，因為現實生活中資源與預算必定有限，因此也可以根據 prediction models 的分析，讓我們可以把資源與預算集中在最有效益的地方。

再次強調，若只有單一的 model 或是研究，其實並沒有辦法做出很肯定的推論。無論是何種類型的研究，都需要大量不同方式反覆驗證過後，才能讓我們在對於不同事物間因果關係的論證有較大的肯定性。

常見研究種類簡介

作者：許承越

    photo credit to: unsplash, UX Indonesia 

我們提出問題並解決問題時，需要做研究來證實我們的想法。在流行病學與生物統計學上，有幾種研究類型，可以讓我們在不同的假設/條件/資源下，可以驗證結果來算出我們的想法。以下依照傳統上認定的效力高低來簡單介紹。

• Meta-analysis 統合分析
• Randomized controlled trial, RCT 隨機對照試驗
• Cohort study 世代研究
• Case-control study 對照研究
• Cross-sectional study 橫斷研究
• Case report/series 個案報告
• Expert opinion/experience 專家意見

Meta-analysis 統合分析

選定主題與假設，利用特定 keywords 尋找可能會用到的同類型、較容易比較之各個論文、統合大小不同 RCT、cohort study 等研究，去分析問題與證明假說。因為一篇 meta-analysis 通常都會用到好幾篇 RCT 來作為統計的依據與論述的證據，所以效力很高。

Randomized controlled trial, RCT 隨機對照試驗

觀察一群背景可能相似的受試者，在接受不同介入方式（可能是不同藥物、治療方式、生活型態調整等等），追蹤與觀察一段時間後，最終的觀察結果有何不同。

重點是藉由統計軟體、亂數表、電腦軟體等進行隨機分配，以讓其他干擾的變數降低。受試者通常會被分配到試驗組（服用新藥、接受新治療）或者對照組（服用安慰劑、或是使用目前的標準治療）。

優點是具有很強的時序性、較好控制我們想要比較的變數、較少回憶偏差，但是最耗費時間資源與人力成本。

又可以分為單盲、雙盲、三盲（ single-blinded、double-blinded、triple-blinded)
單盲是受試者不知道自己被分配到實驗組或對照組、雙盲是受試者與研究人員都不知道誰是試驗組誰是對照組、三盲是受試者、研究人員、執行統計的分析人員都不知道誰是試驗組誰是對照組。

題外話，單盲雙盲這種概念，是由現代統計學與現代演化論之父的英國人費雪發展起來的。傳說中有天費雪先生還在唸劍橋大學時，在陪幾位貴婦喝茶。

他們在爭論到底是把茶加進牛奶、還是把牛奶加進茶裡，哪個會比較好喝呢？後來費雪先生還真的很認真的做了研究；他們還真的把幾位貴婦們的眼睛矇起來，在其他條件都相同的狀況下（茶葉來源、熱水溫度、茶杯、等等）來試驗看看哪一種才是比較好的順序。

單盲雙盲、設定假說、隨機分配等重要統計概念，後來被費雪進一步整理與試驗，最後真的寫出了現代統計學的基礎大作，【試驗設計】這本書。

Cohort study 世代研究

觀察一群背景可能相似的受試者，但跟 RCT 不同的地方在於 Cohort study 並沒有研究人員主動介入或安排治療與藥物使用。Cohort study 是觀察這群受試者一段時間，進而分析一段時間後得出的結果與開始觀察時這些受試者的各個條件與變數，是否有關聯。

例如，觀察一大群背景條件差不多的人，有些有抽煙、有些沒抽煙，觀察一段時間後去看看這些人中得到膀胱癌狀況。優點是有清楚的時序性、相對比較容易推論因果關係、也較不會有 recall bias 等 bais，但缺點是很耗費人力與資源、不太適合觀察罕見疾病。

Case-control study 對照研究

先找到想要探討的健康問題研究方法，透過比較兩個不同群組，一個是有特定的疾病，作為病例組（Case）、而另一組沒有這些特定疾病的試驗者作為對照組（Control），來比較我們要探討的疾病與這些受試者其他背景條件的關聯性。

優點是可以一次分析很多可能病因、所需樣本比較少、跟Cohort study 或是 RCT 比較較為省時省力，但缺點是沒辦法確定因果關係（無法證明誰是因誰是果）、有可能會有 recall bias 。另外若要研究罕見疾病，這是很適合的研究方式，因為若要收案再觀察一群受試者到罕見疾病發病的狀況，實在太慢也太花費時間與資源。

Nested case-control 也是一種不太一樣的應用，利用一個 cohort 中所有已經發病/達到 outcome的受試者作為 cases，而再隨機從其他未發病/未達到 outcome 的受試者中選取 control 來做比對以及研究。

另外也有 case-cohort study 這種折衷方式，就是利用一個 cohort 中找出所有已經發病/達到 outcome的受試者作為 cases，再從 cohort 中隨機選出一個 subcohort，去做比較；通常跟 nested-case-control 相比較有效率。

Cross-sectional study 橫斷研究

研究一組受試者 baseline 的狀況，再去看這些條件與我們欲探討的疾病或 outcome 做比較。我們要探討的因子與疾病都是同一時間存在的。優點是方便、省時省力省資源、但缺點是無法推論因果關係（誰是因誰是果無法證明）、只能探討盛行率（Prevalence）而非發生率（Incidence）。

Case series/report 個案報告

分析特定特別案例，與之前的論文與研究成果做比較，並分析在特病病例上有何學習意義、以及未來可能可以進行的研究方向。

Expert opinion/experience 專家意見

特定領域的專家分享自己的經驗、截至目前為止之研究成果與可能應用方式、未來發展可能等等。

不同的研究方式，各有不同的效力、優點與缺點等。但是無論是什麼我們想要探討的問題，很難有真正單一個研究就可以做出100%正確的因果關係推論。很多我們目前認定的科學知識與見解，都是由大量的研究、統計、與大大小小的錯誤修正中得來的。

課程心得：Health Advocacy

作者：許承越

     photo credit to: unsplash, Miguel Henriques

Advocacy 的意思是：倡議、擁護、鼓吹、主張、辯護。在法律與政策形成過程中，各方利益團體的 advocacy ，會對最終結果有很大程度的影響；其實各種法律與政策的制定，都是不同利益團體/政治力量，多方角力後妥協的結果。公共衛生政策當然也是如此。

Health advocacy 這堂課，是要讓大家了解，如何善用不同資源、研究結果、presentation skills 等等，去影響健康衛生相關的政策與法律制定的過程與結果。

這堂課使用的許多例子，是針對槍械暴力（Gun violence）的 Health advocacy 。授課的老師是 Joshua Horwitz。他是一位律師，也是 Executive Director of the Coalition to Stop Gun Violence。這堂課，使用了很多 Dr. Horwitz 所長期以來研究與倡議的 gun violence 問題。

槍械暴力在美國一直是一個很受關注的公共衛生與健康議題，因為每年都有不少人因為槍支暴力造成健康身體上永久的影響、甚至是死亡。槍支暴力與其延伸出的美國擁槍權，也是長久以來讓支持派與反對派爭論不休的問題。

在以前，若出現隨機/針對特定人士的槍殺、掃射、以及大規模屠殺案，都會被歸咎於「攻擊者具有精神疾病」。

然而，「犯人有精神疾病」這樣長久以來深根蒂固的刻板印象，一來強化了對於精神疾病的污名化，使得精神疾病患者承受更多歧視、壓力、與不平等對待；二來將槍械暴力與攻擊行為歸咎給精神疾病，並沒有辦法幫助我們去釐清造成這些暴力與殺傷行為的成因、也無法幫助我們找到如何預防更多類似事情的方法。

後來，研究指出，在犯下槍支暴力的犯人之中，其實只有很少比例，具有精神疾病病。精神疾病患者會有槍械暴力傷害他人的比例，其實並沒有比一般沒有精神疾病的人，還要來得高。

Dr. Horwitz 的研究團隊，指出了這點，並搜集了大量的資料與研究證據（連結在此：https://pubmed.ncbi.nlm.nih.gov/25211757/）

(McGinty EE, Frattaroli S, Appelbaum PS, et al. Using research evidence to reframe the policy debate around mental illness and guns: process and recommendations. Am J Public Health. 2014;104(11):e22-e26. doi:10.2105/AJPH.2014.302171)

96%的槍械暴力，其實起源於嚴重精神疾病以外的原因。真正有顯著危險要犯下槍械暴力傷害他人的人，其實應該與這個人之前是否出現危險言論、傷害與暴力行為等等有關。

這一系列的研究與倡議活動，讓 Dr. Horwitz 促成了 Consortium for Risk-Based Firearm Policy，結合許多公共衛生與心理健康學者來研究槍械暴力的影響、以及進行槍械暴力的防治政策推薦。這一系列的努力，促成了全美國第一個 Gun Violence Restraining Order law (GVRO)於 2014 年 9 月立法與開始實施。

GVRO 限制槍械子彈的販售，如果有人被家人、同事朋友、警察與執法機關等發現有高危險行為，如暴力行為與恐嚇言論等，進而通報與登記，那麼他就會在一定的時間內無法合法地取得或購買槍械，目前所登記持有的槍械也會被相關執法機關沒收，直到狀況穩定。

在 GVRO 出現之前，美國並沒有特定的法律依據，可以預先阻止特定的人取得槍械甚至沒收已經持有的槍械。

GVRO 接下來也在美國好幾個其他州通過，進而降低了不少槍械暴力、人命損失、家庭破碎的可能。

Dr. Horwitz 與他團隊的努力，讓我很震撼。讓我了解到，有科學研究與數據統計支持的證據，有很大的說服力，甚至可以影響國家政策與法律制定，進而降低了很多人命損失的機會、讓很多家庭可以繼續完整的生活。

其他方法，例如 presentation skills、elevator pitch、以及美國不同層級的立法機構中會有 testimony 的機會，讓相關學者專家、相關事件受影響人、利益團體負責人有可以倡議以及發表想法的機會，進而影響相關的利害關係人與立法者，在這堂課中都有讓我們模擬與練習的機會。

課堂上也有讓我們練習如何針對自己特定有興趣的議題與政策，去做資料的搜集與統整，並寫出一份 policy recommendation 的報告，配合統計結果與研究證據，來提升自己論述的說服力與可信度。

務實的層面，也是讓我很欣賞的部分。

我們常常被鼓勵，做出一個專業的判斷前，需要超脫所謂政治立場，做出超然與客觀的決定。然而，考量現實世界的複雜性，很難有完全超然與客觀的決定。任何事情都會受到政治的影響；而政策與法律，基本上更是多方民意、利益、政治勢力等等多方角力與妥協後的結果。

所以，我們更應該採取一個「立場」。

你想要對一個議題進行倡議，你對這個議題有特定的看法、也希望目前的政策與法律可以往什麼地方發展，那麼這就是你的「立場」。「沒有立場」這件事情，是不可能、也不切實際的。有了自己的立場，才能順利地去 networking、去宣傳、去合作。

認清這件事情，才能更務實地去推動與倡議我們想要爭取的事情，也才能在民意、各方利益、政治勢力角力中盡量維持我們的核心價值、爭取我們要倡議的事情。

如果要看我其他課程的心得，請點這裡的連結：流行病學、生物統計學、與公共衛生筆記。